Effects of Humidity Change on Blackwood

Introduction

Most wooden flutes made today probably are of African Blackwood (aka. Mpingo, Mozambique Ebony or Granadilla).  Like all timbers, it is dimensionally affected by changes in humidity, and changing humidity is a continuing and often significant cause of problems to wooden instruments.  It's useful then to get some idea of how this material is affected by changes in humidity.

Caveat

This is very much a preliminary look at this topic and the results depicted below should not be taken too literally until more work can be done to confirm and explain the effects noted.  

The test pieces

For the test, I chose the 5 pieces that go to make up one of my "Rudall Perfected" model flutes - the head, barrel, left hand section, right hand section and the foot.  The pieces had lain around for a few years in the roughed out state - turned round, a few mm oversize and drilled out, a few mm undersize.  I keep such timber in the workshop in racks of metal wire clothes baskets, so we can be confident that they would be well equilibrated to Canberra's humidity level, which averages 50% most of the time.

Preparation

At the start of the experiment, the pieces were trimmed to final length, reamed to their final bore dimensions and the outside turned to the final profile.  The excess block material was carved away, and slots cut for keys.  The only work remaining to do on the woodwork would be to fit the silver rings to the sockets, ream the bores and sockets a final time and then turn down the tenons to fit.

The test points

I monitored these test points:

• the weight of all five pieces together
• the maximum Inside Diameter of the barrel end of the head
• the minimum Inside Diameter of the barrel end of the head
• the maximum Outside Diameter of the barrel end of the head
• the minimum Outside Diameter of the barrel end of the head

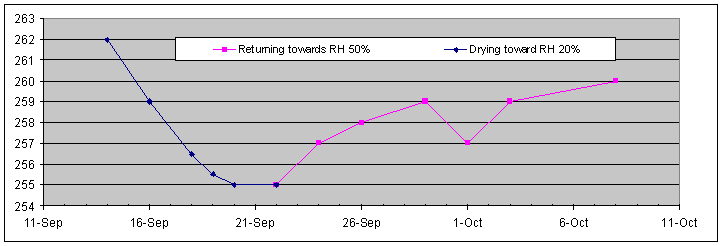
I chose the barrel end of the head as the wood is thin here, and should react relatively quickly to changes in humidity.  It's easily accessed too.

The Experiment

Once the timber had been prepared as outlined above, I put it into a chamber artificially maintained at around 20% relative humidity.  Readings were taken every few days until it was clear that the rate of weight loss had slowed to nothing.  The pieces were then taken from the environment chamber and returned to normal atmosphere.  Again, monitoring continued until the rate of change dropped to around zero.

Change in Weight

The graph below illustrates the changes in weight:

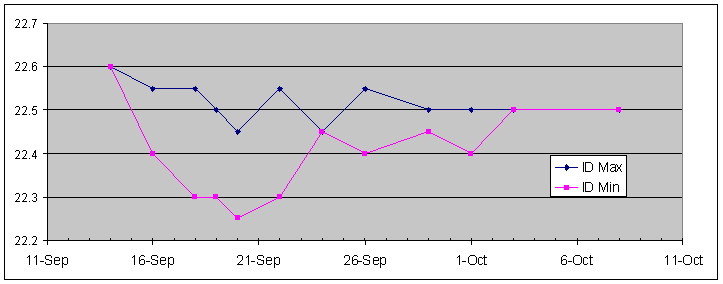
As theory predicts, the changes are exponential - quick at first, slowing as it approaches the target value.  The timber lost 7 grams of moisture in 6 days - quite a bit when we remember 7 grams is equivalent to 7 cubic centimetres, i.e. 7mL - well over a teaspoon-full - just from a 30% change in humidity.  And at quite a high rate - the wood took only 6 days to achieve that change.

On September 22, when the weight hadn't changed in two days, I took the pieces from the chamber and left them out on the bench.  Again, the curve above shows the classic exponential form but not so fast as on the way down.  This is probably reasonable as the humidity in the workshop varies quite a bit during the day, while the humidity in the environment chamber is much more closely maintained.  So the timber is now aiming at a moving target.  Further, the chamber runs around 30 degrees C probably significantly assisting mobility, while the average workshop temperature at this time of year would be 10 to 15 degrees.

In the days around October 1, you can see a short dip responding to a short dry spell in the weather.  As you will see later, this blip is reflected in the dimensional changes too.

You will notice I terminated the experiment before the weight returned to exactly where it started.  I suspect it might never, but might settle down a little under the original weight.  As you will see below, changes in movement seemed to have stopped by then, and, hey, I've got flutes to make!

Changes to inside diameter

The graph below illustrates what happens to the inside diameter over this period:

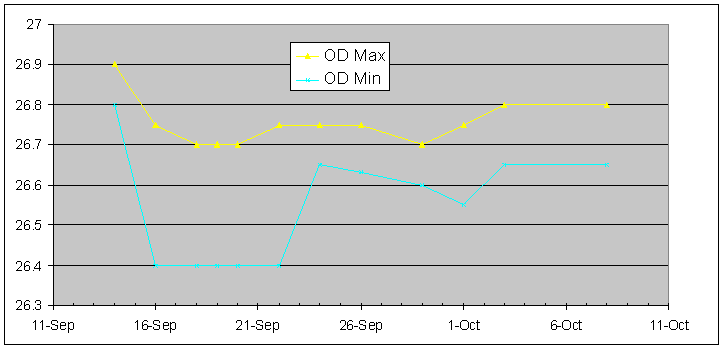
Interestingly, there isn't all that much change to the diameter on one axis (in navy - marked the "Inside Diameter Maximum") - it waffles about a bit, finally ending up about 0.1mm (0.004") smaller than when it started.  But it doesn't seem to take much notice of the period in the drying chamber.  

The other axis ("Minimum Inside Diameter) does change though - quickly dropping 0.35mm during the 6 days in the chamber, but returning just as quickly to meet the maximum when finally re-equilibrated to the humidity it was acclimatised to at the time of reaming.  Note it even manages an obliging little downward blip on October 1.

Changes to Outside Diameter

So what was the outside of the timber doing all this time?

Again, the "Maximum Outside Diameter" axis didn't get all that excited - dropped 0.2mm but regained half that after the torrid period.  But check out the "Minimum Outside Diameter" axis.  Dropped like a stone over the first two days then remained steady until taken out of the chamber.  Then zoomed back to its final diameter within two days, apart from taking part in the October 1 blip.

Interesting also that the two axes (maximum and minimum diameters) started off a little different and ended up a little more different, unlike the inside diameters which started off and ended together.  No immediate explanation for that other than perhaps stresses in the wood relieving.  The inside was cut first with a reamer, then the outside turned with the wood held between cones.  So it had to be round and concentric at the end of the cutting process.  The first measurements would have taken place within hours of that, but already it had moved a bit.  We needn't get too worried though, the difference is only 0.15mm - about 0.4% of diameter and certainly not visible to the eye or of any acoustic significance.  Interesting though ...

Observations

So we find that weight change behaves pretty much as expected, although perhaps more quickly.  This is thin wood though - about 4mm wall thickness and with access to atmosphere inside and out - so it's quite a different thing to a solid lump of timber.  And it does have to be remembered that this wood had not been oiled or otherwise "sealed", so we might expect the finished flute to gain and lose weight more slowly.  But then again, think of the onslaught of moisture when the flute is played for several hours.  And consider the far greater seasonal changes in say parts of North East US with extremely humid summers and three months of snow in winter - perhaps a change closer to 80% rather than the 30% we've simulated.  So our test is really quite gentle.

It's in the dimensional stability that we find more surprises.  Now, conventional cabinet-maker experience is that timber shrinks about twice as much on the tangential face (of the growth rings) as on the radial face.  This obviously relates to our findings but is not the same.  We see little or no change in one axis (our maximum diameters), but fast and significant changes to the opposing axis (our minimum diameters).  

Now perhaps this shouldn't surprise us.  In the cabinet-maker's solid lump of timber, there is the rigid centre acting to minimise movement.  But in our flute, the centre has gone, leaving the remaining outer ring of timber great freedom to meander where it chooses.

We can perhaps imagine this mechanism at work.  Picturing the cross-section of the cylinder of wood as a ring, imagine it has shrunk a little and is now uniformly a little smaller in all directions.  Now squeeze it across one axis so that the dimensions return to original on the other.  We now have an egg whose maximum diameter has not changed from the original value, but whose minimum diameter is significantly less.

Extrapolation

It's interesting to speculate on what all this might mean if it can be safely extrapolated to old cocus flutes.  Made in dank 19th century London, then carried around the world and subjected to harsh continuous central-heating in climates with long snow seasons, they crack miserably.  While this is obviously the result of shrinkage being resisted by the head and barrel liners, perhaps it's even more the result of eccentric shrinkage and the very unequal stresses caused by eccentric shrinkage being thus resisted.  Indeed, there might even be an element of cumulative fatigue from the effects of annual eccentric cycling doggedly resisted by cylindrical metal liners.  

So, not just shrinkage, but shrinkage resisted.  More than that, asymmetrical shrinkage symmetrically resisted.  Perhaps even more, the cumulative effects of the stresses thus caused.

If a cumulative mechanism is at work, it might explain why flutes continued to be made in the same way for so long in the 19th century - perhaps the problems didn't surface until quite a while later.  It might mean we may be in for some unpleasant surprises when enough years elapse to see its effect on modern day lined flutes.  

Ovality in old flutes?

And perhaps it goes some way to explaining another paradox.  First time you measure an old flute you notice that the bore is not round but to some extent oval.  The penny drops soon enough - it's clearly caused by shrinkage that is not equal tangentially and radially.  

Now it has often been suggested that the old cabinet-maker's 2:1 ratio should give us all the information we need to re-establish the original dimensions accurately.  We just need to measure the maximum and minimum diameters at every desired interval along the bore, subtract them to get the difference, add the difference to the maximum (or twice the difference to the minimum) and, Bob's Yer Uncle, we magically arrive at the long-lost original value.

Well, Robert might be Your Mother's Brother, but he ain't no use to man or beast.  The figures you arrive at employing that technique are just laughably absurd.  The piece would be so much bigger that they could never have got the rings on it, the tenons would be jammed in their sockets, and the tuning slides would have rattled around and fallen out!

Our findings here might suggest why the results are ludicrous - the 2:1 rule just isn't applicable to thin cylinders of wood.  And it also suggests that averaging maximum and minimum figures is not the way to go - that will give results that are distinctly too small.  Indeed, the results would seem to validate the approach I've been taking with bore measurements - look for the maximum diameter by rotating the T-gauge until it achieves maximum penetration at the current setting .  According to the results above, that's the most accurate figure you're going to find and not significantly less than the original.

Too long between drinks?

Or, to guarantee the best results, we should re-hydrate the flute until the bore is restored to circularity before taking the measurement.  "What?", sputters the head conservator, "our flutes are carefully maintained to 50% +/- 5% and you want to drop them in a bucket of water for a week?!"  

Well, perhaps something a little less violent, but think about it.  We know that old flutes, particularly those constrained by slides, rings, socket linings, key posts and shafts suffer miserably at humidities below those they were built at.  We'd actually be doing those flutes a real favour to find out what humidity that was, and return them to something at least approximating it.  And, as our test suggests, each flute has its own historical hygrometer built in to assist us to get it right.  

Matters outstanding

It's one of the cruel paradoxes of experiments that you only find out how they should have been conducted when you finish.  It would be worth repeating the experiment, firstly to ensure that this was not a rogue piece of timber with unusual proclivities (unlikely, as the ovality discussion suggests).  It would be good to relate firmly the maximum and minimum diameters with the tangential and radial faces.  A dial indicator and a rotary head could give us a fuller picture of shape of the distortions, with readings taken say at every 10 degrees of rotation.

And ranging over a wider range of humidity (e.g. 90% to 10%) would be desirable, especially if the timber could be allowed to acclimatise and readings taken at every 10%.  Ideally too, a number of cycles should be followed through, to see if hysteresis (lag or memory effect) plays a part.  And, while this test measured dimensional change at the end of the piece, it would be good too to monitor change at the middle of a piece.  We could expect this to be slower, but by how much?  And how does oil or other bore sealing methods effect the rate of transfer?  And perhaps, in a parallel experiment, strain gauges on each axis could monitor the kinds of forces that would be exerted by such shrinkage and tell us what we're expecting this material to withstand.

Sigh, when do we find time for such studies?

Back to McGee Flutes home page