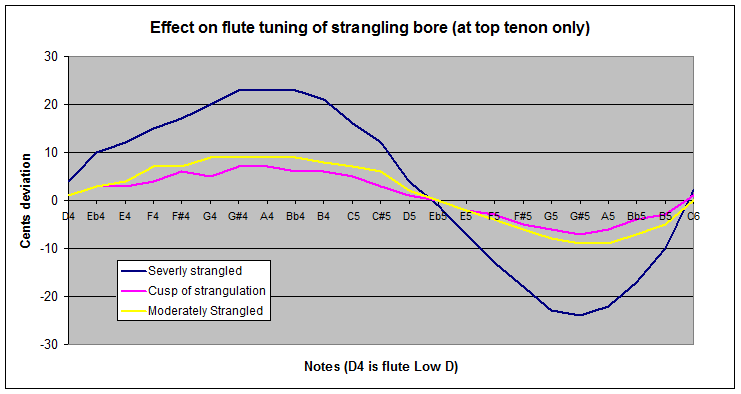
Effects of Thread Wrapping series:

Analysis

Introduction

In our first article in this series, we looked for signs of strangulation and bore compression among old flutes and found plenty. Time now to consider some of the implications of what we found.

Willis' Secret

What was Willis' secret? How come his 190 year old flute seems to have survived unscathed, while earlier and later ones have suffered compression or even strangulation? The answer is actually pretty obvious on inspection. Willis' tenon is thicker than those on more recent flutes. Indeed, it's more reminiscent of a baroque flute, although that didn't seem to have helped our boxwood baroque instrument!

Unfortunately, the solution available to Willis is no longer attractive to us. In Willis' time, flutes were generally much thicker all along, and bores were thinner. The outside of the barrel at the base of his socket is 29.7mm, the inside diameter 23.5mm. The tip of the tenon is 23mm, the inside at that point 18mm. Since then, it's been realised that a thinner head plays more adroitly, and bigger bores give more power. As the flutes became thinner (all over, for more elegant appearance and comfort in holding), and the bores bigger, the wall strength was whittled down from both sides. And as the strength of a piece of wood varies at approximately the square of its thickness, a small reduction in thickness brings a bigger reduction in strength.

Willis had a second trick, and I suspect this has even more to do with his freedom from damage. He also made the thread trough very shallow - so shallow that the current fairly thick thread has room for one layer only. This thread is 0.4mm (estimated under the microscope) and, from its condition, is probably not original. Less thread to cause the damage, more tenon wall to resist it. Bravo, Mr Willis!

Indeed, here's an interesting observation. Supposing you deepen Willis' thread trough just enough to accept a second layer of thread. And you might have good reason to - as it stands there isn't much room there to accommodate any wood movement due to seasonal change. The second layer of thread will double the constraining force on the tenon, and accommodating it will slightly weaken the tenon's strength to resist that force. A third layer would treble the force, and weaken the tenon further. The ratio of thread depth to timber left might be the critical element in Mr Willis' legacy.

This seems to be confirmed when we contrast the unscathed Willis with two of the worst affected flutes in the survey - the strangled boxwood and cocuswood flutes. They both had very slim barrels, around 28mm, leaving little room for all that has to fit inside. But the Schuchart from the Bate seems to have pretty juicy dimensions (34mm OD and 24.8 ID in the middle of the socket, around 22.5 and 17.2 for the tenon) and yet its tenon is dramatically crushed. Confirming it may not be enough to consider wood strength alone, but necessary to look to the ratio of that and threadband thickness. The Schuchart's tenon is so distorted we might never be sure what thread thread depth was supposed to be. But the current difference between the socket's 25mm ID and the tenon's 22.5mm OD suggests that a lot of thread would be needed to fill that gap. I'd suggest serial strangulation might be the killer here - see the discussion on this topic later.

What effects can we expect?

We can expect at least two kinds of ill-effects due to strangulation. There will be an increase in aerodynamic losses, as the oscillating air column encounters an increased constriction in the middle of the flute. So performance will be down on that basis.

But there will also be a marked acoustic effect which will evidence itself in two ways. Tuning is going to be different to what the original maker expected, and, if the spacing between the octaves changes enough, that is likely to bring a weakening of performance, as the harmonic alignment will suffer back at the jet.

I ran a few computer simulations to predict what we might expect. The software I'm using is currently being developed by a group involving the Physics Department at the University of New South Wales, the Powerhouse Museum and myself. It's not quite ready for complete de novo computer modelling of flutes yet, but more than adequate for comparative analyses like this, where only relatively small changes are involved.

You'll see three traces in the graph below:

The blue trace is the severely strangled boxwood flute we met at the top. You'll see that the model predicts sharpening of the low octave, to a startling 24 cents around low A, and a flattening of the second octave, again by up to 24 cents around 2nd octave G#. With those midrange octaves now being narrowed by up to 48 cents, we can certainly expect significant loss of performance, as well as distinctly odd tuning!
The yellow trace shows what a moderately strangled flute such as the Richard Potter will suffer. Same general shape, but with a bit less than half the effect. I'd still expect some performance loss from both acoustic and aerodynamic sources.
Finally, in pink, a flute that was on the very cusp of strangulation, i.e. the bore is sufficiently compressed to flatten the taper under the wrap, but not enough to actually cause a measurable bottleneck. But enough to narrow the G# octave by about 14 cents. That may or may not be enough to introduce acoustical misalignment losses - this would depend largely on luck.

I could model more of the flutes, but it would mostly serve to confuse the graph. They can be expected to come out between the pink and blue traces. A flute like my Rudall Carte that only shows mild compression would come out between the pink trace and the horizontal axis. That's about as much uninvited change as I'd like to see.

Now that we see what the computer models predict, we should try to confirm the prediction with differential RTTA. That will certainly be on my agenda next time I work on a seriously strangled flute.

We can draw much from these simulations:

Note the general shape of the tuning change is one we are already familiar with. Most old flutes have LH notes that tend sharp in the low octave. A lot of that is attributable to other reasons, but it's certainly not something to be encouraged further!
There isn't that much between the Cusp and Moderately strangled flutes. Once the bore has compressed enough to negate the taper, significant errors are already being introduced. Which is logical enough. The maker tapered the flute to bring the octaves into line. If part of the taper gets cancelled, so does that part of its beneficial effect.
Given that we found above that most old threaded flutes were strangled or beyond, we can now say that most old flutes no longer perform as the maker intended.
If we have an old flute that is at the cusp or moderately strangled, we have to ask ourselves what are we doing to prevent the problem advancing.
In the serendipitous event that bore compression to your flute actually improved the tuning, you'd still have to wonder about an aerodynamic downturn. Put another way, a bullet in the head is one cure for headache; it may not be the best.

Just how strong is thread?

I took a length of the thread taken from the strangled cocuswood flute, supported it from a retort stand, tied the free end to a hook, and carefully added calibrated weights until the thread broke. I got to 700 gms weight, or 1.5lb. That's pretty strong for a thread with a diameter of about 0.1mm!

I measured the thread from the Richard Potter "somewhat strangled" flute. This was very old thread, and no doubt weakened by time and compression. It also broke at 700 grams weight, but unless we can find a modern equivalent, we don't know what it was capable of when young and fresh. There were 5.4 metres of that thread on the top tenon. It was squashed too flat to measure by normal mechanical means, but using a stage micrometer on the zoom microscope, I'd estimate it as varying between 0.3mm and 0.9mm, depending if I was looking on the flat or the side. It had become a ribbon, rather than a thread. If we took the average of 0.6, it's 6 times thicker than the modern sewing thread.

I also measured some "soft-looking" yellow hempy sort of thread I'd bought 30-odd years ago from a Scottish bagpipe shop, sold for the express purpose of wrapping tenons. It measured about 0.3mm on the stage micrometer. A single length of that broke at 2.7Kg (6lb). Thread is strong!

Another useful observation I can make about these tests is that none of the threads seemed "elastic", in the bungee cord sense. When the first calibrated weight went on, the thread straightened out. As I added more weights, there was no sense of the thread getting longer, up to the point where it broke. I can obviously measure this if needed, but I suspect the observation is enough. A coil of a hundred or more turns of any of these threads will present a formidable barrier to expansion.

Calculating the forces

An informal attempt to calculate the possible maximum forces involved lead to numbers so great that some readers rejected them outright as preposterous! I asked my friend Professor Neville Fletcher for a confirmation (reproduced below in italics). Characteristically thorough, he responded with two ways of looking at it - the total force applied by the thread on the tenon, and the pressure the thread applies to the tenon. You'll remember that pressure is force divided by area, and so takes into account the area covered by the wrap.

Total force applied to tenon

From what you write, you want to evaluate the total effective inward force acting on the tube. Suppose the string is tightened to 700 grams weight and that there are 13 layers each of 150 wraps. Now imagine that you slice along the tube on both sides and remove one half of all the threads, but that magically the thread stays in place and taut. To make this happen you have to put a weight of 700 grams on each end of each of semicircular wrap. This makes a total weight of 13 x 150 x 700 grams or 1365 kg on each end of the semicircle, making 2,730 kg altogether.

For US readers, this translates to 6020 pounds.

Pressure applied to the tenon

If the question you are answering is "What is the effective compressive pressure provided by the winding?" Then each turn has an inward force of T/R per unit length, where R is the radius of that turn, acting over a length 2.pi.R, giving a total inward force of 2.pi.T. (Note that this is independent of R.) If we have N turns in a single layer and M layers. then the total inward force is 2.pi.N.M.T. But this force is spread over a total area 4pi.N.R'.r where R' is the average radius of the winding and r is the radius of the thread, so the inwards force per unit area, or equivalently the inwards pressure, is (2.pi.N.M.T) / (2.pi.N.R'.r) = (M.T) / (R'.r). To evaluate this you need to decide whether to use SI units and get the answer in pascals. Doing it on the back of an envelope, I get about 2x10^8 Pa or about 2000 atmospheres.

For US readers, this translates to about 29,000 psi.

These are indeed frightening figures. But keep in mind the following:

we based the thread tension on the breaking strain of the thread. It's unlikely that anyone would wind that hard. But even if they wound at one tenth that tension, one tenth of those forces is still a lot to apply permanently to a thin-walled tube of wood.
I'm told that this is no news to serious kite flyers. It seems that, if you wind up the kite string onto a hollow plastic reel at the tension the kite is exerting, the reel can crack and collapse under the accumulated force!
The moment you apply anything like that pressure to the tenon, it will start to compress. And will continue to compress until it takes off enough pressure that it can support the remainder of the force. In other words, it will crush to reach equilibrium. We will see that happen at the start of the experiment below.
A more realistic way to look at these figures is that they represent the maximum resistance to expansion that the threadband (even if relatively loosely wound on) could present before the thread would break. As we'll see later, that is totally relevant.
The actual value of force applied to a real tenon is not really calculable, because of all the unknowns. But it suffices us to know that it is more than enough to cause problems!

Conclusions so far

In this section, we've seen that it may well be the ratio of the thread band depth and the thickness of the underlying timber that determines how much compression occurs. We've seen that flutes on the cusp of strangulation (i.e. flattened taper, but no bottleneck) are about as distorted as we'd like to go. By inference, any flute where a bottleneck can be detected is more distorted than we would like. And a look at threads and some calculations arising leave us in no doubt that thread presents a serious danger to tenons and therefore flutes.