Hysteresis?
|
||
But it's been worrying me ever since.
Certainly it's not unreasonable to expect wood to exhibit hysteresis
- plenty of natural things do. But surely someone would have
noticed before this and we'd be on the lookout for this behaviour?
Surely it would seem a bit odd for our flutes to be one size
after the rainy season and another after the dry.
Then again, we've become accustomed to our flutes being one size
in the rainy season and another in the dry, so maybe we
just don't notice? Or is some other effect responsible for
this unexplained behaviour? Whatever, I felt we couldn't leave
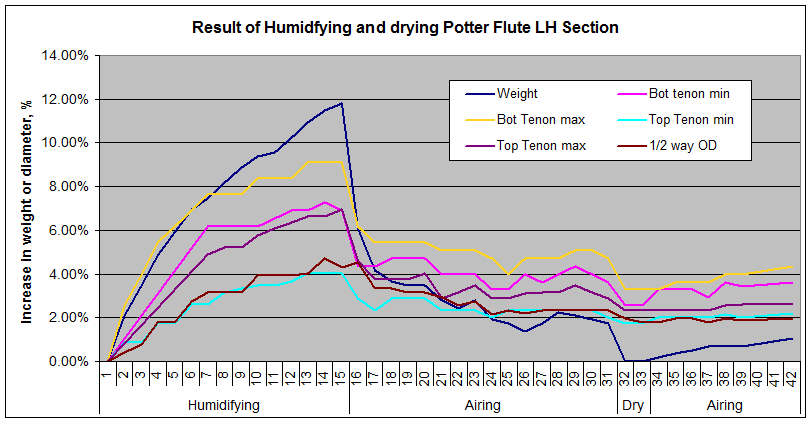
it there, so this article picks up where Plan B left off. The story so farLet's quickly recount the story so far. (If you want the full action replay, go back to Plan B.) Essentially, we had taken the LH section, weighed and measured it carefully, then submitted it to water-saturated air for 15 days. You can see the results in the graph below. It's weight increased by nearly 12%, and its various dimensions by between 4 and 9%.
Then we let it air for 16 days, in which the weight it had gained (the water content) dropped back to 2% and the dimensions not quite so far, to between 2 and 5%. But neither dropped back to zero. A little puzzled, I forced the weight down to the original value by exposing it to dry air. The weight went down, but the dimensions stayed larger by from 2 to over 3%. Further, when I let it air on the bench again, the weight increased by about 1%, and the dimensions ended up between 2 and 4%. Curiouser and curiouser, cried Alice.
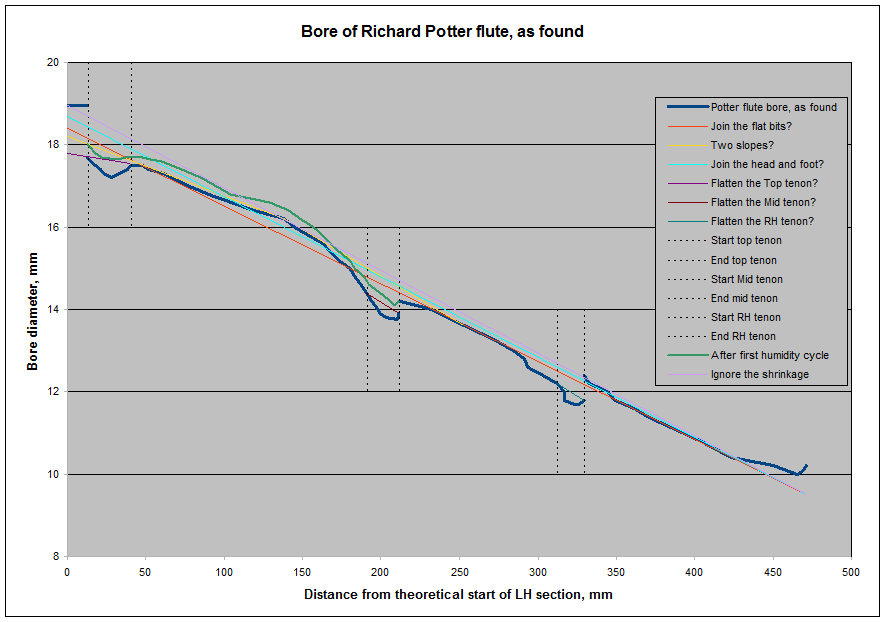
When we carefully re-measure the LH section, we confirm it has increased
in diameter for its full length (see graph below, pea green versus navy
blue). So, no room for denial, but no easy explanation either. All
very odd! So, what now?I came up with a fiendish plan. Let's really dry this flute section out, then let it return to equilibrium with the atmosphere. If hysteresis is involved, we should see it settle at a weight and dimensions less than the original measurements, just like, when we made it very wet, it settled on values higher than the original. Hysteresis by definition. If that doesn't happen, we have to look elsewhere. I've brought some new weaponry to bear in my fight against flute ignorance. The McGee Flute Laboratories now boasts a desiccator and enough desiccant to suck a whole can of beer to powder. (I can say this with equanimity only because I'm a wine drinker!) It's 7%RH in there! In she goes, for a holiday in New Mexico..... What happens?We can see the result in the graph below. In order to make it easy to compare with the hydrating experiment Plan B, I've used the same reference points, and tacked the new results on the end of the old graph. The start of our new experiment is Drying, Day 0.
You'll see after 9 days of drying that the weight is down to 4% less than the start of the original experiment, indeed 4% lower than it's been throughout. Yet the dimensions are levelling out at around 0 to +1%. Hey you, he yells, tapping aggressively on the walls of the desiccator - you're supposed to be down in the negative, down there with the weight. No answer came the stern reply.... Well, he consoled himself. Let's just see what happens when we let the moisture return. Let's air the section and see where it ends up. But, it has to be said - it's not going to look good for the hysteresis theory if we can't manufacture some hysteresis! Sure enough, as soon as we return it to the wild, the piece gathers weight and size (Airing, Day 10 to 18). Some squally damp weather has blown in from the sea, so there's plenty of nice moisture in the air, even inside the workshop, to replenish that sucked out by the desiccant. As we'd expect, the weight increases, as the desiccated wood thirstily laps up whatever the air can supply. And the dimensions rise accordingly. So, that pretty well wraps it up for the hysteresis theory. If hysteresis was the ruling mechanism, the dimensions should have gone below zero and remained below zero even after the weight had normalised. But the dimensions are remaining doggedly above zero. That's not to argue that there is no hysteresis, just that any hysteresis is far overridden by another, more significant force. So now, the challenge - what is that force? I think I have an idea, but it's going to take some believing... Alternative theoryIf you get the impression I'm reluctantly being dragged toward the alternate theory, it could be because I fear your reaction. Because the alternate theory is quite far-fetched and quite far-reaching. I'd like to be able to offer a range of alternate options, but explanations that fit the facts are few on the ground. Let's just remind ourselves what the facts are. We took the Potter LH section, removed its lappings, and hydrated it dramatically - to the point where it gained 12% in weight. When we let it air, neither the weight nor the dimensions returned to the starting point. We suspected that hysteresis (memory effect or path dependency) might have been involved, but the current experiment found no sign of it. What else could be a possible explanation? Leaning heavily on Occam's Razor (mixing metaphors in a manner likely to result in personal injury), we come to this. The thread lappings were not just compressing the tenons. They were not just compressing the tenons and the areas adjacent to the tenons. They were compressing the tenons, the areas adjacent to the tenons, and the rest of the whole section! So, when the lappings were off, and we rehydrated the section, it all increased in diameter. It went back to normal, or at least, it went in the direction of normal. But not only was that compression reducing the dimensions of the section, but also its capacity to hold moisture. That seems a little harder to get your head around, but perhaps the old "bundle of straws" metaphor can help us. Imagine the piece of wood is a bundle of straws. We find the bundle can soak up a certain amount of water. We bind the ends tightly, compressing the bundle into a barrel shape. Can it absorb quite so much water now? RamificationsOK, not so hard to believe, you say from the protection of your own bunker. But consider the consequences of accepting that explanation. It suggests that any flute that exhibits what I've been defining as mild strangulation (oh, na´vetÚ!) is probably also shrunken along its entirety. With what effect, one wonders. Without doing some computer modelling (and you can tell that's got to be on the horizon), I'd expect it to flatten the lower octaves relative to the upper. Add some extra constrictions at the three tenons and we might well have plausible explanations for many of the otherwise inexplicable syndromes that old flutes present, like flat foot, wide octaves, etc. Woah! And consider the modern flute maker. Many, particularly those who make flutes for early music, recommend returning their instruments after blowing in for re-reaming. Why should a recently made flute need re-reaming? Assuming well-seasoned wood to start with, it could only be because something is compressing the timber. Moisture from playing would enlarge the flute, making the reamer rattle around, and not cut anything. What could be compressing the timber? The thread wrapping is the only candidate in sight. You can see reason behind my caution. I got in enough trouble at the start of Series One just alleging that thread lapping could compress tenons. Now I'm arguing it compresses whole flutes. If I had any sense of self-preservation, I'd do the experiments first and reveal the answers later. Not conduct the experiments in real-time in public! I'm way out on a limb, and I'm sawing it off... Another museBack in the 19th century, when flutes like these roamed the earth, scientists and inventors were still grappling with basic issues. Indeed, the very word "scientist" wasn't coined until the 1830s. Darwin, Pasteur, Edison, Bell, Bunsen, Curie, Doppler, Hertz, Tesla and Thomson (a.k.a. Lord Kelvin) are just some of the well-known names. In the acoustics field, Helmholtz and Lord Rayleigh. No nuclear magnetic resonance machines, CT scanners, mass spectrometers, chromatographs, tokomaks, particle accelerators, scanning electron microscopes, radio telescopes or data acquisition systems back then, just hand measuring tools and simple lab equipment. But what a foundation they laid! Now we find ourselves one to two hundred year later, looking at the musical instruments of their time, and the awful thought forms - this work could have been done back then! Sure, the beam balance has been upgraded to a digital strain gauge, and a datalogger monitors my environment replacing the wet & dry thermometers. An infrared thermometer measures surface temperatures, and electronic tuners of various kinds replace the old resonance jars and Schreiber's newly-fangled tonometer. And the spreadsheet sure speeds up calculations and presentation. But that's not the point - I'm back at the starting point, just as they were, living the excitement of 19th century discovery. Not for me, the umpteenth decimal point of modern science. Like my period predecessors, I'm dealing with plain yes and no. ConclusionsWoah, where do we go to from here? We have asserted boldly, not so much because we're convinced, but because we're running out of options. But we're hanging all of this on one manifestation. Shouldn't we confirm that this is repeatable behaviour? And ideally, see if another method of hydration will bring a similar result? And even get back to our planned series of experiments. That's the point of making plans, isn't it? On to PlanD, or Back to McGee-flutes Index page...
|