The Experiment
I decided to make up two short tubes, as identical as possible, wrap one
with thread but not the other, and then submit them to the usual
harrowing environmental conditions that abound in my lab.
Casting around the workshop, I found just the scrap piece I needed.
It was an off-cut of the African wood Mopane, which had been obtained
well seasoned in 2002, and was therefore guaranteed to be very well
seasoned by now. Mopane was attractive for this experiment as it
is highly figured, making it easy to determine which is the radial face
and which the tangential. My only concern was that it appears a
waxy wood, and I wondered if that might make it slow on the uptake and
release of moisture. As it turns out, that doesn't seem to be the
case.
In order to make two samples as similar as possible, I resolved to cut
them adjacently from the same piece. I chucked the piece and,
using a boring bar, bored the end out to 19mm (3/4") diameter. I
then turned the outside down to 21mm, leaving a wall thickness of 1mm.
Before separating the two samples with an extremely fine bandsaw blade,
I ran an ink line down the inside on one of the tangential faces, so I
could always realign the faces. The bold grain pattern assured
that I could always realign them end to end. The two pieces ended
up 14mm long (just over 1/2").
I measured the radial and tangential diameters of each, and then, as
intended, wrapped one of them with 100 turns of thin (~0.1mm) sewing
thread.
The theory
Before relating what happened, it would be good to
rehearse what we might expect to happen, given the usual
cabinetmakers' experience of wood under varying climatic conditions.
Wood, as you know, grows on trees, and trees are generally round.
The very heart of these dense trees is rarely sound, and further,
trying to dry this slow-drying wood "in the round" usually meets
with serious splitting. So, logs are intentionally split or
cut lengthwise as soon as possible after harvesting. That
means the blanks for our flutes come from one side or the other of
the split, and therefore of the centre.
We see that when we look at the end grain of a flute
blank. The growth rings run across from one side to the other,
usually in an obvious curve, as these trees are pretty small.
Once we've turned the blank round and smoothed the outside, we can
easily identify two types of faces. The two tangential faces
have broad "cathedral spire" markings, while the radial faces have
fine straight lines, being the ends of the growth rings.
The usual "rule of thumb" is that the radial face
moves much less with change in temperature than the tangential face,
with 2:1 being the usually quoted ratio. That's why guitar and
harpsichord makers carefully select "quarter sawn" timber (the fine
radial pattern) for their sound-boards. It's not uncommon for
a metre-wide (3') harpsichord soundboard to vary over 6mm
(1/4") in width between dry and wet weather. Cut in plank
(tangential) mode that would be a staggering 1/2" or 13mm!
So, as our test samples suffer alternate dehydration
and humidification in the lab, we can reasonably expect them to go
oval, first one way, then the other. To keep track of their
movements, I assigned them compass bearings. I marked the
tangential faces N & S, and the radial faces E & W. The
interesting thing for me is what do they do when they are allowed to
return to normal intermediate relative humidity.
A possible complication
Before we delve into the results, I should just warn
you of a little complication. The cabinetmakers' theory I
outlined above would have us expect that the greatest movement would
be observed on the tangential face. But I have observed over
the years many flutes that appear to have ovalled along an axis
diagonal to the radial and tangential axes. So, I'm going to
be alert to circularity in general, and follow any leads.
The outcome
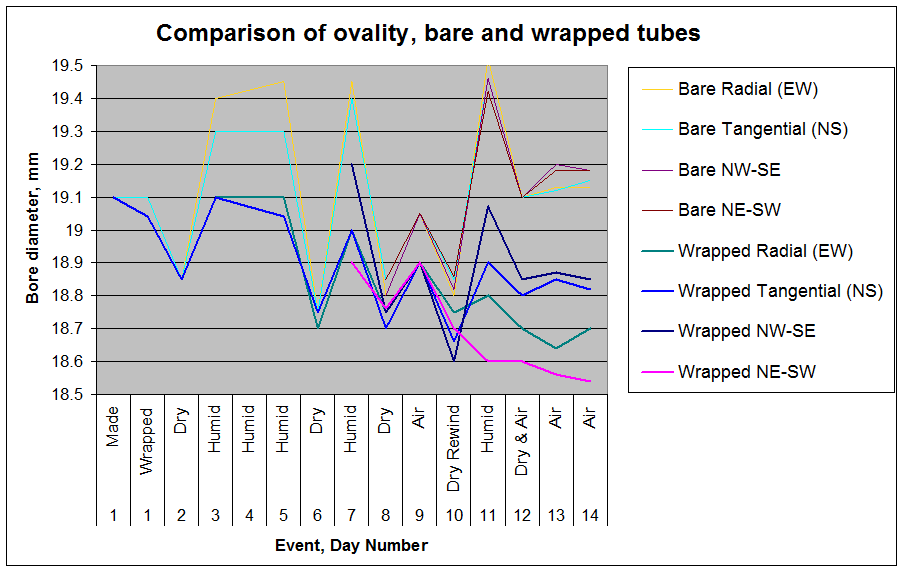
The graph below sets out what happened. At the
beginning, I followed the two axes (radial and tangential) of each
tube. The thin lines are for the bare tube, the thick for the
wrapped.
On Day 1, I made the tubes, and as you can imagine,
they measured the same. I then wrapped one of them, and we can
see a small degree of compression set in immediately, as shown in
the second column, Wrapped. I then put the two tubes in the
Desiccator, at about 15%RH.
On Day 2, you can see that both dimensions of both
tubes have shrunk to the same degree. The tubes then went into
the humidity chamber at over 90%RH.
Day 3, we see that the bare tube (thin lines) has
expanded well above its original dimensions. There is some
evidence that the radial axis has become bigger than the tangential
axis, which seems contrary to expectations.
But, the real story is being told by the wrapped
tube. The tube tried to expand, but that expansion is totally
cut off at the original diameter by the thread wrapping.
Great, you might applaud! The wonderful thread has halved the
pesky expansion of the timber in damp conditions. Bravo!
But keep reading ....
Remembering my suspicions about the waxy-looking
Mopane, I wanted to make sure that this was about as far as
humidification would go, so I left the pieces in the chamber for two
more days. Not much further action, so 1 day per event seems
like a reasonable speed to take things from here on. So, now,
into the desiccator again.
Day 6, after drying, shows that the two tubes are
still free to shrink, although interestingly, the lapped tube has
shrunk a little more than the bare tube. Back into the
humidifier!
On Day 7, I started to notice something quite
interesting. The bare tube had expanded back up to about where
it was on the previous humidification cycle, and it remained
surprisingly round (both axes the same). So much for the
quoted 2:1 ratio! But the wrapped tube had stopped expanding
below its original diameter. Further, although its two
main axes were still the same as each other, I could easily detect
ovality with the callipers. But it wasn't along the main axes,
but diagonally to them!
So, I resolved to start logging these diagonal
dimensions on the wrapped tube also. You'll see they start on
Day 7, in thick pink and thick navy, marked with the compass
bearings NW-SE and NE-SW. And you can see why I could hardly
ignore them - they are 0.3mm different! Time to go back into
the desiccator...
Day 8, and both tubes have shrunk again under the
action of the dry air in the desiccator. The bare tube back to
its normal dry dimensions, the wrapped tube somewhat smaller.
The four axes of the wrapped tube were back closer together, i.e.
the degree of ovality had faded. What was also interesting is
that the wrap on the wrapped tube was now quite loose, and could be
easily slid en masse around the tube. Wow!
I thought this was about the time to find out what
the outcome would be if we let them both equilibrate to atmosphere.
As you can see, on Day 9, the outcome was unspectacular. The
bare tube went back pretty much to original dimensions, while the
wrapped tube was compressed, but not oval. Drat, was this
whole experiment a waste of time?
Serial Strangler Needed!
About then, a little voice said to me, maybe we need
to try some serial strangulation? But was this the right time?
Of course by this time, the wrap was tight again. Then the
penny dropped. You don't need to tighten the wrap on your
thread-wrapped flute in normal weather. It only comes loose in
dry weather, and that's when you do it! We need some drier
weather. Back into the drier!
I resolved at this time to also start measuring and
logging the diagonal dimensions of the bare tube, even though I
hadn't detected any significant ovality. You can see the thin
extra pair of lines starting Day 9. I've replicated the graph
below so you can more easily follow the action.
Day 10, the tube is dry and the wrapping loose.
Once more the bare tube descends to its usual dry dimensions, once
more the wrapped tube shrinks even smaller. And ovality is now
becoming noticeable even in the dry condition. I take the wrap
off and rewind it on, before popping both tubes into the humidifier.
Day 11, after 24 hours of humidification, a
fascinating picture emerges. The bare tube has moved up to its
wet weather dimensions, with a very minor amount of ovality showing.
But the wrapped tube has gone bananas. Only one diagonal,
NW-SE, has even approached the original dimension. The
tangential axis has tried but been arrested 0.2mm lower. The
radial ditto, except 0.3mm lower. But the other diagonal,
NE-SW, is now a full half millimetre less than original, and all
this when the bare tube is 0.4 to 0.5mm engorged! Bare tube
ovality 0.1mm, wrapped tube ovality nearly 5 times greater!

OK, definitely time to let these tubes air and see
where they end up. To save time, I give them both a short
burst in the desiccator until the bare one was close to original
dimensions, then let them both air on the bench. I wait a few
days to make sure they have landed.
Day 14, and the bare ring is now back to just over
the original size. The weather had been dry at the start of
the experiment but we've had 105mm (4") of rain over the last few
days, so that probably explains the slight but negligible size
increase. Ovality negligible at about 0.05mm.
But it's been all downhill for the wrapped ring.
The average of the four axes is now 0.375mm smaller than originally,
with ovality about 0.31mm. Again, the maximum ovality is
centred on the diagonal axes rather than the orthogonal axes
predicted by the theory. And all this within 2 weeks, with
fewer than five humidity cycles.
So, what's going on here? How could this
possibly happen?
Probably because of ....
Anisotropy
Ooh, now there's a new word to bandy around at the session. But
what could it mean?
Anisotropy is just the opposite of isotropy, if that helps! And
isotropy means equal in all directions (from the Greek iso = equal and
tropos = direction). So anisotropy simply refers to something
having qualities that are directionally dependant.
The something here is wood, specifically our wrapped tube. Wood has three dimensions of interest to us. The
length, the radial and the tangential (to the growth rings) planes in
wood all exhibit quite different qualities.
And the quality we're probably finding unequal is stiffness. The wood in
one horizontal plane (as the tree stands) is less stiff than the wood in the
other horizontal plane. So, when force is applied equally around
our tenon (by the thread wrap), one plane is better able to handle it than the
other, so the
tenon goes ovoid.
But why diagonal?
That, I will concede, is not so easy to explain. I can think of
several possible factors:
-
the wood in the diagonal planes of a thin tube
is the least stiff
-
the curvature of the growth rings favours one
diagonal over the other
-
the direction of the wrap puts more stress on
one diagonal
A more colloquial explanation might be that when an
irresistible force meets an immovable object, things usually go
pear-shaped! What is actually going on is perhaps one for the
material scientists and of little import to us; what concerns us is
the fact that just one case of serial strangulation has caused our
test ring to compress suddenly and go elliptical!
Myth Busted!
Note that this busts a claim long put forward by proponents of thread wrapping
- that the tight wrap of thread is somehow beneficial in keeping the
tenon round. In fact, the tight wrap of thread exploits weakness
in the wood to make it oval!
Is ovality bad?
Not in reasonably mild cases. If taken to extreme, it could cause
air leakage around the tenon, difficulty rotating the flute sections,
etc. It shouldn't have acoustical ramifications, unlike the bore
compression which has to have acoustic ramifications.
Is ovality good?
It's sometimes argued that ovality is beneficial to the operation of a
flute. This probably arises from a claim that making the vertical
axis of the head deeper assists with the breath "getting around the
corner". I'm not aware that this claim has ever been tested, and
even if so, it would seem to only apply in the head region.
Clearly for the tuning slide and sockets to work, the tubing further
down the flute needs to be round by that point.
Even if ovality of the head were proven to noticeably improve the
performance, the maker would want control of the amount and direction,
not to leave it up to forces beyond our control.
Is ovality inevitable?
I don't know, and we shouldn't extrapolate that far from this initial
experiment. But it was certainly interesting that, in our previous
experiment compressing both ends of a tube, the end that compressed the
most also ovalled the most. We now need to observe strangled and
unstrangled flutes to see if ovality is more common in the strangled
case.
An anisotropic speculation
We saw above that thread wrapping a tenon leads to ovalling of the tenon
and adjacent body, as the tenon wrap forces exploit anisotropic
stiffness in the timber. Could other forces, e.g. a tight metal
ring, do the same? My guess is probably, but probably to a lesser
extent. One would expect the metal ring (assuming it was round
when it went on) would have some finite stiffness of its own, unlike the
thread wrap. It's not a question this study is concerned with, as the
Potter flute doesn't have metal rings. It does have ivory rings, although
these are not normally installed under pressure. But the question is much
complicated by the nature of ivory, which almost assuredly will have
anisotropic qualities of its own. Depending on how the ring is
installed, these might line up and reinforce or partially negate the
wood's tendencies. And timber and ivory will have different rates
of expansion vs humidity. I think we just might leave that
complexity for another day ....
Conclusions
The experiment
demonstrates that thread wrapping is certainly capable of reducing
the normal movement of wood with changes in the weather, but at a
price. It causes bore compression and it sends the wood oval.
More dramatically, the experiment illustrates the frightening power
of serial strangulation. A single change of thread, carried
out at the logical time - when dry weather makes the thread loose -
was enough to convert compression to strangulation. The need
for rethreading probably gives us our first clear warning sign that
a flute is succumbing to pressure.
The experiment will also
be a confidence boost to those who felt the original test tenon
experiment should have been accompanied by a "control" tenon.
The bare tenon came through the experiment unscathed, despite being
cycled over a greater range of dimensions in a short time frame.
It was the wrapped tenon that suffered, clearly proof that the wrap
was the game-changer.
Back to McGee-flutes
Index page...
Created 28 June 2011
|